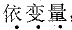 ,习惯上用Y表示。以横轴代表自变量X,纵轴代表依变量Y,可以将一群观察事物的两种关系在坐标图上以P(X,Y)的方法定位,作出一群点图,便可在体上看出两者的关系,例如图22-1。
,习惯上用Y表示。以横轴代表自变量X,纵轴代表依变量Y,可以将一群观察事物的两种关系在坐标图上以P(X,Y)的方法定位,作出一群点图,便可在体上看出两者的关系,例如图22-1。第二十二章 相关回归分析
提要 相关回归的意义,原理;小样本的直线相关和回归分析;相关系数和回归系数的意义及假设检验;应用直线相关和回归分析时的注意事项。
在医学上,许多现象之间都存在着相互联系,例如身高与体重,体温与脉搏,年龄与血压,钉螺与血吸虫感染等。而有些事物的关系是互为因果的,如上述钉螺是因,感染血吸虫是果;但有时回果不清,只是伴随关系。例如父母的兄弟,兄高,弟也可能高,但不能说兄是因、弟是果,这里不是因果关系,而可能与社会条件、家庭经济、营养、遗传等因素有关。
相关是解决客观事物或现象相互关系密切程度的问题,而回归则是用函数的形式表示出因果关系。有相关不一定因果关系;反之,有因果关系的,一定有相关。我们称“因”的变量叫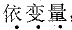 ,习惯上用Y表示。以横轴代表自变量X,纵轴代表依变量Y,可以将一群观察事物的两种关系在坐标图上以P(X,Y)的方法定位,作出一群点图,便可在体上看出两者的关系,例如图22-1。
,习惯上用Y表示。以横轴代表自变量X,纵轴代表依变量Y,可以将一群观察事物的两种关系在坐标图上以P(X,Y)的方法定位,作出一群点图,便可在体上看出两者的关系,例如图22-1。
图22-1(A)表示血压(依变量)随年龄(自变量)增长而增高,其图像性质与(B)一样称正相关(positive correlation);图(C)的依变量随自变量的增加而减少,称为负相关(negative correlation);若二者没有关系,则称无相关(如图D、E、F)。
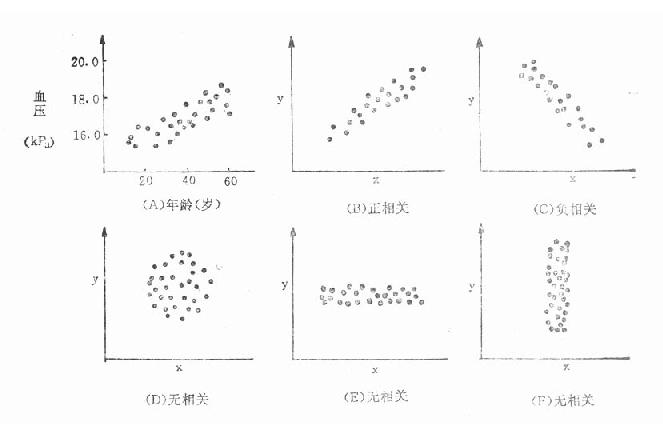
图22-1 年龄与血压相关(A)和五种有代表性点图(B~F)
根据实际资料,用数学的方法求出一条曲线(或直线),使我们能够从一个自变数推算出相关的依变量的值,这条线就叫回归线。回归线有直线和曲线两种。本章仅介绍直线相关与回归分析。
例22.1 某产科医师发现产妇尿液中雌三醇含量与初生儿体重有相关现象,因此检查了31例待产妇24小时的尿雌三醇含量,并记录下各产儿初生体重,统计如表22-1。作者意欲通过测定尿中雌三醇含量以间接预测初生儿体重,以便对低出生体重儿采取预防性措施。
表22-1 待产妇尿雌三醇含量与初生儿体重统计
| 编号(1) | 尿雌三醇mg/24h(2) | 初生儿体重kg(3) | 编号(1) | 尿雌三醇mg/24h(2) | 初生儿体重kg(3) |
| 1 | 7 | 2.5 | 17 | 17 | 3.2 |
| 2 | 9 | 2.5 | 18 | 25 | 3.2 |
| 3 | 9 | 2.5 | 19 | 27 | 3.4 |
| 4 | 12 | 2.7 | 20 | 15 | 3.4 |
| 5 | 14 | 2.7 | 21 | 15 | 3.4 |
| 6 | 16 | 2.7 | 22 | 15 | 3.5 |
| 7 | 16 | 2.4 | 23 | 16 | 3.5 |
| 8 | 14 | 3.0 | 24 | 19 | 3.4 |
| 9 | 16 | 3.0 | 25 | 18 | 3.5 |
| 10 | 16 | 3.1 | 26 | 17 | 3.6 |
| 11 | 17 | 3.0 | 27 | 18 | 3.7 |
| 12 | 19 | 3.1 | 28 | 20 | 3.8 |
| 13 | 21 | 3.0 | 29 | 22 | 4.0 |
| 14 | 24 | 2.8 | 30 | 25 | 3.9 |
| 15 | 15 | 3.2 | 31 | 24 | 4.3 |
| 16 | 16 | 3.2 |
资料来源:Rosner B:Fundamentals of Biostatistics P.346,Duxbury Press,1982
一、相关分析(correlation analysis)
先将上表数据按直角坐标作出图22-2。从该图的点子分布可以看出,尿中雌三醇浓度愈高,新生儿体重愈大;这群点子的分布基本上呈直线趋势。
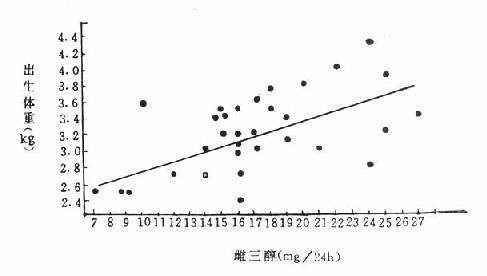
图22-2 待产妇尿雌三醇含量与产儿出生体重相关图
(一)相关系数(correlation coefficient)
相关系数是表示两个变量(X,Y)之间线性关系密切程度的指标,用r表示,其值在-1至+1间。如两者呈正相关,r呈正值,r=1时为完全正相关;如两者呈负相关则r呈负值,而r=-1时为完全负相关。完全正相关或负相关时,所有图点都在直线回归线上;点子的分布在直线回归线上下越离散,r的绝对值越小。当例数相等时,相关系数的绝对值越接近1,相关越密切;越接近于0,相关越不密切。当r=0时,说明X和Y两个变量之间无直线关系。计算相关系数的公式为:
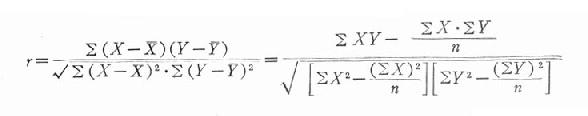
为了获得公式22.2中各数据,先将表22-1资料进行计算如表22-2。
从表22-2的计算获得
ΣX=534 ΣX2=9876 ΣY=99.2 ΣY2=324.18 ΣXY=1750
N=31
按这些数据进一步以下演算求r。
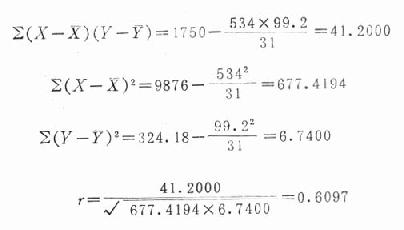
(二)相关系数的假设检验
本例题31例,只是总体中一个样本,由此求得的相关系数,必然存在抽样误差。总体相关系数为零(ρ=0)时,从这总体中抽出31例,因为抽样误差,r也可能不等于0。氙以要判断该样本r是否有意义,需与总体相关系数,ρ=0比较,看两者的差别有无统计不学意义。
相关系数的假设检验,可用t检验,公式如下:
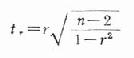 公式(22.2)
公式(22.2)
自由度v=n-2
H0:ρ=0
H1:ρ≠0
α=0.05
本例r=0.6097,n=31,代入公式(22.2)
表22-2 相关系数计算表
| 尿雌三醇X(mg/24h)(1) | X2(2) | 初生儿体重Y(kg)(3) | Y2(4) | XY(5) |
| 7 | 49 | 2.5 | 6.25 | 17.5 |
| 9 | 81 | 2.5 | 6.25 | 22.5 |
| 9 | 81 | 2.5 | 6.25 | 22.5 |
| 12 | 144 | 2.7 | 7.29 | 32.4 |
| 14 | 196 | 2.7 | 7.29 | 37.8 |
| 16 | 256 | 2.7 | 7.29 | 43.2 |
| 16 | 256 | 2.4 | 5.76 | 38.4 |
| 14 | 196 | 3.0 | 9.00 | 42.0 |
| 16 | 256 | 3.0 | 9.00 | 48.0 |
| 16 | 256 | 3.1 | 9.61 | 49.6 |
| 17 | 289 | 3.0 | 9.00 | 51.0 |
| 19 | 361 | 3.1 | 9.61 | 58.9 |
| 21 | 441 | 3.0 | 9.00 | 63.0 |
| 24 | 576 | 2.8 | 7.84 | 67.2 |
| 15 | 225 | 3.2 | 10.24 | 48.0 |
| 16 | 256 | 3.2 | 10.24 | 51.2 |
| 17 | 289 | 3.2 | 10.24 | 54.4 |
| 25 | 625 | 3.2 | 10.24 | 80.0 |
| 27 | 729 | 3.4 | 11.56 | 91.8 |
| 15 | 225 | 3.4 | 11.56 | 51.0 |
| 15 | 225 | 3.4 | 11.56 | 51.0 |
| 15 | 225 | 3.5 | 12.25 | 52.5 |
| 16 | 256 | 3.5 | 12.25 | 56.0 |
| 19 | 361 | 3.4 | 11.56 | 64.6 |
| 18 | 324 | 3.5 | 12.25 | 63.0 |
| 17 | 289 | 3.6 | 12.96 | 61.2 |
| 18 | 324 | 3.7 | 13.69 | 66.6 |
| 20 | 400 | 3.8 | 14.44 | 76.0 |
| 22 | 484 | 4.0 | 16.02 | 88.0 |
| 25 | 625 | 3.9 | 15.21 | 97.5 |
| 24 | 576 | 4.3 | 18.49 | 103.2 |
| 534 | 9876 | 99.2 | 324.18 | 1750.0 |

V=31-2=29
查t值表,t0.01(29)=2.756,本例tr=4.1423>t0.01(29),P<0.01,按α=0.05水准拒绝H0,接受H1,可以认为临产妇24小时尿中雌三醇浓度与初生儿体重有正相关关系。
如果不用t检验,可以根据v查相关系数r界值表(附表22-1)。本例v=29,查表得知r0.01(29)值为0.456,而本例r=0.6097>r0.01(29),故P<0.01,与上述t检验的结果一致。
二、回归分析(regression analysis)
医学上,不少娈量间虽存在一定关系,但这种关系不象函数关系那样十分确定。例如正常人的血压随年龄而增高,但这只是总的趋势,有些高龄人的血压却不一定偏高;一群正常人按年龄和血压两个变量在坐标上的方位点,并非集中在一条上升直线上,而是围绕着一条有代表性的直线上升。
直线回归分析的任务在于找出两个变量有依存关系的直线方程,以确定一条最接近于各实测点的直线,使各实测点与该线的纵向距离的平方和为最小。这个方程称为直线回归方程,据此方程描绘的直线就是回归直线。
(一)直线回归方程式(linear regression equation)的计算
直线回归方程的通式为:
=a+bX 公式(22.3)
式中Y为自由变量X推算因变量Y的估计值,a为回归直线在Y轴上的截距,即X=0时的Y值;b为样本回归系数(regression coefficient),即回归直线的斜率(slope或称坡度),表示当X变动一个单位时,Y平均变动b个单位。如果已知a与b,用以代入公式(22.3),即可求得直线回归方程。求a和b的公式分别为:

公式(22.4)
公式(22.5)
对样本中两个变量分析,不但可作相关分析,还可进一步作直线回归分析。仍以表22-1为示范,该例经过直线相关分析,r=0.6097,两变量间有直线关系,从相关系数计算时,已求得:
Σ(X-x)(Y-Y)=41.2000
Σ(X-x)2=677.4194
而 Y=ΣY/n=99.2/31=3.2000
x=ΣY/n=534/31=17.2258
代入公式(22.4)
b=41.2000/677.4194=0.0608
代入公式(22.5)
a=3.2000-0.0608×17.2258=2.1527
代入公式(22.3)
=2.1527+0.0608X
(二)样本回归系数的假设检验
样本回归系数也有抽样误差问题,故需对b作假设检验,以评估b是否可能从回归系数为零(即β=0)的总体中随机抽得的。
检验步骤:
H0:β=0 即b是由β=0的总体中随机抽样的样本回归系数。
H1:β≠0
α=0.05
t检验:检验公式为
tb=|b|/sb 公式(22.6)
式中sb是回归系数的标准误,计算公式为
 公式(22.7)
公式(22.7)
式中sy.x为各观察值Y距回归直线(Y)的标准差,是当X的影响被扣除后Y方面的变异指标。可用以下公式计算:

公式(22.8)
公式(22.9)
本例上述已算得
Σ(X-x)2=677.4194
Σ(Y-Y)2=6.7400
Σ(X-x)(Y-Y)=41.2000
分别代入公式(22.9),(22.8),(22.7)和(22.6)得
Σ(Y-Y)2=6.7400-41.20002/677.4194=4.2343
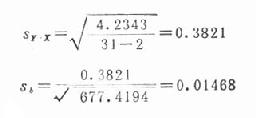
tb=0.0608/0.01468=4.1417
分析评价 本例自由度v=31-2=29,查t值表,t0.01(29)=2.756,P<0.01,按α=0.05检验水准,拒绝无效假设,可以认为待产妇24小时尿中雌三醇含量与初生儿体重之间存在直线回归关系。
(三)描绘回归直线
根据以上求得回归方程Y=2.1527+0.0608x,可以在自变量X的实测范围内(本例为7~27)任取X1和X2两值代入上式求得在图22-2中的P1(X1,Y1)和P2(X2,Y2)两坐标点,将两点连结为一直线,就属该方程的回归直线。作图要注意的是P1、P2两点最好距离远些,绘出的直线在坐标上误差就小些。
三、应用直线相关与回归分析时的注意事项
1.作相关与回归分析要有实际意义,不要把毫无关联的两个事物或两种现象作相关、回归分析。
2.两事物或现象间有相关,不一定有回果关系,也可能仅是伴随关系。但是,如果两事物或现象间存在因果关系,则两者必然是相关的。
3.相关与回归分析所说明的问题是不同的,但又是有联系的。相关表示相互关系,回归表示从属关系。可以证明,同一批资料所算得的r与b的检验统计量(tr,tb)是相同的,如本章的案例前后算得的tr=tb=4.14。由于相关系数的计算及假设检验比较方便,故可用相关系数的显著性检验取代回归系数的显著性检验。事实上在作回归分析之前,一般先作相关分析,而只有在确定了两变量间有直线关系的前提下,求回归方程及回归线才有意义。
4.相关与回归的应用,仅限于原实测数据的范围内,而不能随意外推。因为不知道在此范围之外,两变量间是否仍存在同样的直线关系。如果确有进行外推的充分根据和需要,亦应十分慎重。
5.在X与Y均呈正态变量时的加归分析中,由X 推算Y与由Y推算X的回归系数及回归方程是不同的,切勿混淆。
附表22-1 相关系数显著性界值表
| v | R0.05(v´) | R0.01(v´) | V´ | R0.05(v´) | R0.01(v´) |
| 1 | 0.997 | 1.000 | 24 | 0.388 | 0.496 |
| 2 | 0.950 | 0.990 | 25 | 0.381 | 0.487 |
| 3 | 0.872 | 0.959 | 26 | 0.375 | 0.478 |
| 4 | 0.811 | 0.917 | 27 | 0.367 | 0.470 |
| 5 | 0.754 | 0.874 | 28 | 0.361 | 0.463 |
| 6 | 0.707 | 0.834 | 29 | 0.355 | 0.456 |
| 7 | 0.666 | 0.798 | 30 | 0.349 | 0.449 |
| 8 | 0.632 | 0.765 | 35 | 0.325 | 0.418 |
| 9 | 0.602 | 0.735 | 40 | 0.304 | 0.393 |
| 10 | 0.576 | 0.708 | 45 | 0.288 | 0.372 |
| 11 | 0.553 | 0.684 | 50 | 0.273 | 0.354 |
| 12 | 0.532 | 0.661 | 60 | 0.250 | 0.325 |
| 13 | 0.514 | 0.641 | 70 | 0.232 | 0.302 |
| 14 | 0.497 | 0.623 | 80 | 0.217 | 0.283 |
| 15 | 0.482 | 0.606 | 90 | 0.205 | 0.267 |
| 16 | 0.468 | 0.590 | 100 | 0.195 | 0.254 |
| 17 | 0.456 | 0.575 | 125 | 0.174 | 0.228 |
| 18 | 0.444 | 0.561 | 150 | 0.159 | 0.208 |
| 19 | 0.433 | 0.549 | 200 | 0.138 | 0.181 |
| 20 | 0.423 | 0.537 | 300 | 0.113 | 0.148 |
| 21 | 0.413 | 0.526 | 400 | 9.098 | 0.128 |
| 22 | 0.404 | 0.515 | 500 | 0.088 | 0.115 |
| 23 | 0.396 | 0.505 | 1000 | 0.062 | 0.081 |