 公式(21.1)
公式(21.1)第二十一章 秩和检验
提要秩和检验是一种非参数统计方法。用于配对资料、两组资料以及多组资料的比较。
前面讨论的u检验、t检验和方差分析都是假定样本的数据来自正态或近似正态分布的总体。在实际工作中往往碰到非正态资料或不了解现有的数据来自何种分布。秩和检验(rand sum test)是一种非参数统计(nonparametric statistics)方法。此法可用于多种总体分布或分布不明确的情况,因此适用范围广。缺点是没有充分利用资料所提供的信息,当资料适用参数统计却用了非参数法处理时,常损失部分信息,降低检验效率。
第一节 配对资料的比较
一、符号检验(sign test)
此法主要用于配对资料的比较,现以表21-1资料为例介绍其方法步骤。
例21.112名宇航员行前及返航后24小时的心率变化如表21-1所示,试问航行对心率有无影响?
表21-1宇航员航行前后的心率(次/分)及符号检验计算表
| 宇航员编号(1) | 航前(2) | 航后(3) | (2)-(3)差数的符号(4) |
| 1 | 76 | 93 | - |
| 2 | 71 | 68 | + |
| 3 | 70 | 65 | + |
| 4 | 61 | 65 | - |
| 5 | 80 | 93 | - |
| 6 | 59 | 78 | - |
| 7 | 74 | 83 | - |
| 8 | 62 | 79 | - |
| 9 | 79 | 98 | - |
| 10 | 72 | 78 | - |
| 11 | 84 | 90 | - |
| 12 | 63 | 60 | + |
(一)建立检验假设
H0:宇航对心率无影响,即差值的“正”、“负”号个数相等
H1:宇航对心率有影响,即差值的“正”、“负”号个数不等
α=0.05
(二)将各对数据中,航前大于航后者记为“+”,航前小于航后者记为“-”,航前等于航后者记为“0”,列于表21-1第(4)栏。
(三)分别数出“+”“-”号的个数,并以“+”号的个数作为a,“-”号的个数作为b ,代入式(21.1)
 公式(21.1)
公式(21.1)
本例a=3,b=9
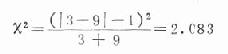
v=1,x20..05(1)=3.84,今x2=2.083<3.84,P>0.05,按α=0.05检验水准不拒绝H0,因此尚不能认为宇航对心率有影响。
二、符号秩和检验(Wilcoxon法)
符号等级检验(signed rank test)是上述方法的改进,是在观察“+”“-”号个数的基础上亦考虑差值的大小,通过对差值偏秩求和进行检验的,故效果较好。仍以例21,1介绍其方法步骤。
表21-1宇航员航行前后的心率(次/分)比较
| 宇航员号(1) | 航前(2) | 航后(3) | 差值(4)=(2)-(3) | 秩次 | |
| +(5) | -(6) | ||||
| 1 | 76 | 93 | -17 | 9 | |
| 2 | 71 | 68 | 3 | 1 | |
| 3 | 70 | 65 | 5 | 4 | |
| 4 | 61 | 65 | -4 | 3 | |
| 5 | 80 | 93 | -13 | 8 | |
| 6 | 59 | 78 | -19 | 11 | |
| 7 | 74 | 83 | -9 | 7 | |
| 8 | 62 | 79 | -17 | 10 | |
| 9 | 79 | 98 | -19 | 12 | |
| 10 | 72 | 78 | -6 | 5 | |
| 11 | 84 | 90 | -6 | 6 | |
| 12 | 63 | 60 | 3 | 2 | |
| 合计 | 7 | 71 | |||
(一)建立假设
H0:宇航对心率无影响,即差值的总体中位数M=0
H1:宇航对心率有影响,即差值的总体中位数M≠0
α=0.05
(二)求各对数值的差数如表21-2第(4)栏
(三)编秩按差值的绝对值由小到大编秩,将秩次按差值的正负分两栏,如表21-2第(5)、(6)栏。注意:编秩时,遇有几个绝对值相等、符号相反的差值时,各取平均秩次;符号相同的相等差数,可不必取平均秩次;遇有差值为0的,则弃去不计,随之从相应的对子数n中减去。
(四)确定统计量t 分别求正负秩次之和,以绝对值较小者为统计量T,如表21-2第(5)、(6)两栏的合计。本例T=7。
(五)确定P值,作出推论
1.查表法用于对子数n≤25时,根据对子数n查附表21-1符号秩和检验临界值表。若现有统计量T值大于表中相应的界值T0.05,则P>0.05;若现有统计量小于或等于表中相应的T0.05,则P≤0.05。本例对子数n=12,查表得T0.01=7,本例T=7,故P=0.01,按α=0.05检验水准拒绝H0,可认为宇航对心率有影响,使心率增快。由此看出符号秩和检验比符号检验效率高。
2.正态近似法对子数n>25时,按式(21.2)计算统计u值。
 公式(21.2)
公式(21.2)
因统计量为u值,按表19-3所示关系作出判断。