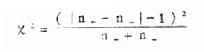 ,v=1(10.1)
,v=1(10.1)第二节 符号检验
将资料用正负号表示,然后根据正负号个数计算χ2值进行假设检验,称为符号检验。符号检验的检验假设:若为成对资料,则为H0:P(X1>X2)=P(X2>X1),含义是总体内每一对数字(分别用X1和X2表示)中,X1>X2的概率等于X2>X1的概率,都是1/2,而备择假设H1为P(X1>X2)≠P(X2>X1)≠1/2;若为不成对资料,检验假设H0为F(X1)=F(X2)即两总体的分布函数相等,而H1:F(X1)≠F(X2)。符号检验的计算都很简单,但检验效率也较低。
一、成对资料的比较
现以例10.1说明其计算步骤如下:
1.划出每对数值的正负号,如令用药后每分钟灌流滴数大于用药前的为“+”,反之为“-”,相等为“0”,则其结果见表10.1最右侧栏。
2.清点“+”、“-”、“0”各有几个,分别记为n+、n-、n0,得n+=9,n-=3,n0=0
3.代入式(10.1),求得χ2值
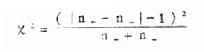 ,v=1(10.1)
,v=1(10.1)
4.但χ2值表,作出结论。
例10.1 表10.1为豚鼠注入肾上腺素前后的每分钟灌流滴数,试比较给药前后灌流滴数有无显著差别。
表10.1 豚鼠给药前后的灌流滴数
| 豚鼠号 | 每分钟灌流滴数 | X2-X1的正负号 | |
| 用药前X1 | 用药后X2 | ||
| 1 | 30 | 46 | + |
| 2 | 38 | 50 | + |
| 3 | 48 | 52 | + |
| 4 | 48 | 52 | + |
| 5 | 60 | 58 | - |
| 6 | 46 | 64 | + |
| 7 | 26 | 56 | + |
| 8 | 58 | 54 | _ |
| 9 | 46 | 54 | + |
| 10 | 48 | 58 | + |
| 11 | 44 | 36 | - |
| 12 | 46 | 54 | + |
将n+=9,n-=3代入式(10.1)得

χ20.05,1=3.841,今χ2<χ20.05,1,故P<0.05,不能拒绝检验假设H0,故这种相差是不显著的,不能得出用药后比用药前灌流滴数增加的结论。
此法简便,但较粗糙,数据少于6对时,不能测出显著性,12对以下应慎用,当达到20对以上时,其结果才比较可靠,另外,n。较多时,会夸大差别。
二、不成对资料(两组或多组)的比较
现以例10.2说明其计算步骤如下:
1.各自排列,统一编秩号。将两组数据分别从小到大排列,然后按两组数据自小至大统一给以顺序号,即为秩号。编秩号时,凡数据相等而分属于两组的,应编平均秩号,如0.042共有三个,分属于两组,其秩号应该是7、8、9,求其平均,皆给以平均秩号8。
2.求秩号的中位数MR,公式是:
 (10.2)
(10.2)
3.求各组n+、n-、n0:以MR为准,大于MR的秩号个数为n+,小于MR的秩号个数为n-,相等者为n。
4.代入下式求χ2值
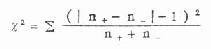 ν=组数-1 (10.3)
ν=组数-1 (10.3)
5.查χ2值表,作结论。
例10.2 表10.2为9名健康人和8名铅作业工人的尿铅值(mg/L)试比较两组间有无显著差别?
表10.2 9名健康人与8名铅作业工人的尿铅值(mg/L)
| 健康人 | 秩号 | 铅作业工人 | 秩号 |
| 0.001 | 1 | 0.042 | 8 |
| 0.002 | 2 | 0.042 | 8 |
| 0.014 | 3 | 0.048 | 10 |
| 0.020 | 4 | 0.050 | 11 |
| 0.032 | 5 | 0.082 | 14 |
| 0.032 | 6 | 0.086 | 15 |
| 0.042 | 8 | 0.092 | 16 |
| 0.054 | 12 | 0.098 | 17 |
| 0.064 | 13 |
两组各自排队,统一编秩号,其结果见表10.2
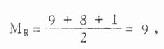 以此数为准,数得两组秩号的n+、n-、n0如
以此数为准,数得两组秩号的n+、n-、n0如
下:
| n+ | n- | n0 | |
| 健康人数 | 2 | 7 | 0 |
| 铅作业工人组 | 6 | 2 | 0 |
代入公式
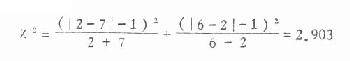
ν=2-1=1,χ20.05,1=3.841
今χ2<χ20.05,1故P>0.05 不能拒绝检验假设,相差不显著,还不能说健康人与铅作业工人尿铅值有显著差别。
当多组资料比较时,其步骤与两组比较的一致,但计算χ2值的公式略有不同:
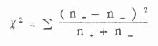 (10.4)
(10.4)
符号检验未充分利用原始资料中的全部信息,故比较粗,但因其简便,可迅速得到结果故也有其使用价值。