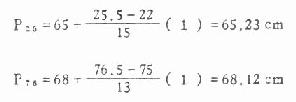
第二节 变异指标
一、变异指标的意义及种类
设有甲乙两人,对同一名患者采耳垂血,检查红细胞数(万/mm3),每人数五个计数盘,得结果为
| 合计 | 均数 | ||||||
| 甲 | 480 | 490 | 500 | 510 | 520 | 2500 | 500 |
| 乙 | 440 | 460 | 500 | 540 | 560 | 2500 | 500 |
两人计数的均数都是500,能说两人的检验技术相同吗?不能,因为甲的计数结果比较密集,而乙的分散,因此甲的检验精度显然比乙的高。从上可以看出:描述一群变量值,除用平均数等表示其集中位置外,还要说明其分散或变异情况。说明变异情况的特征值称变异指标。变异指标的种类较多,下面分别介绍极差、四分位数间距、均差、方差、标准差及变异系数。
1.极差 最大值与最小值之差称极差(或全距),符号为R,是变异指标中最简单的一种。如上例甲计数的极差为520-480=40,乙的为560-440=120。可见乙的计数较甲的波动大。一般把最小值与最大值写在括号里,附在极差的后面。如上例写成40(480~520)与120(440~560)。其单位与变量值的相同。
当调查例数增多时,遇到较大或较小极端值的机会就加大,因此最大值与极差随着例数的增多而加大,但最小值却随着例数的增多而变小。
极差计算简便,但只考虑了最小、最大值,因此易受个别极端值的影响,且随例数的多少而变动,不稳定。仅用于粗略地说明变量值的变动范围。但在正态分布中可用以估计标准值范围,详见有关文献。
2.四分位数间距 极差的不稳定主要是受两极端数值的影响,于是有人将两端数据按比例去掉一定例数,这样所得数据就比较稳定了。例如两端各去掉25%,取中间50%数据的数值范围,那么只要计算P25与P75,求P75与P25之差即得四分位数间距,符号为Q。
Q=P75-P25 (4.12)
例4.7 试计算表4.8七岁男童坐高的四分位数间距
求 P25的位置102×.25=.25.5.
求 P75的位置102×.75=.76.5.
求累计频数得:
L25=65,L75=68,
A25=22,A75=75,
f25=15, f75=13, i=1
表4.8 7岁男童的坐高
| 坐高(cm) | 例数(f) | 累计频数 |
| 61- | 1 | 1 |
| 62- | 3 | 4 |
| 63- | 4 | 8 |
| 64- | 14 | 22 |
| 65- | 15 | 37 |
| 66- | 21 | 58 |
| 67- | 17 | 75 |
| 68- | 13 | 88 |
| 69- | 7 | 95 |
| 70- | 5 | 100 |
| 71- | 2 | 102 |
| 合计 | 102 | — |
代入式(4.5)得:
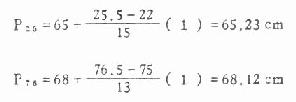
Q=68.12-65.23=2.89 cm
有50%的7岁男童,坐高在65.23~68.12cm之间,其四分位数间距为2.89cm。
3.均差 四分位数间距虽比极差稳定,但仍只是两点之间的距离,没有利用每个变量值的信息。于是有人计算每个变量值与均数(或中位数)差的绝对值之和,然后平均称为均差(或平均直线差)作为变异指标之一。
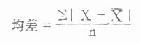 (4.13)
(4.13)
例4.8 试计算4.3中,心重的均差。
由例4.3知X=293.75g,代入式(4.13)得

4.方差 式式(4.13)中用变量值与均数之差的绝对值之和∑∣X-X∣,而不用离均差之和∑(X-X)是因为∑(X-X)=0,不能说明变异情况,故取绝对值以去掉负号。亦有人用平方的办法,即用离均差平方和∑(X-x )2,既去掉了负号,又提高了指标的灵敏性。因为数值愈大,平方后增大的愈多,所以离均差稍有变化,就能从指标上反映出来。例如有甲乙两组数据如下:
| X | ∑∣X-X∣ | ∑(X-X)2 | ||||||
| 甲组 | 10 | 11 | 12 | 13 | 14 | 12 | 6 | 10 |
| 乙组 | 9 | 12 | 12 | 13 | 14 | 12 | 6 | 14 |
乙组仅有两个数据与甲组的不同,这种不同从∑∣X-X∣或均差上是反映不出来的,但从∑(X-X)2上却反映出来了。以∑(X-X)2组成的变异指标有方差与标准差。方差是标准差的平方,将在第八章讨论,下面先介绍标准差。
二、标准差
1.标准差的公式 样本标准差是用得最多的变异指标,其公式为
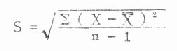 (4.14)
(4.14)
式(4.14)中的n-1是自由度。n个变量值本有n个自由度,但计算标准差时用了样本均数X,因此就受到了一个条件即∑X= nX的限制。例如有4个数据,它们的均数为5。由于受到均数为5的限制,4个数据中只有3个可以任意指定。如果任意指定的是4、3、6,那么第4个数据只能是7,否则均数就不是5了。所以标准差的自由度为n-1。
2.标准差的计算
(1)按基本公式(4.14)计算
例4.9 用例4.3资料计算心重的标准差。
已算得X=293.75g,代入式(4.14)得
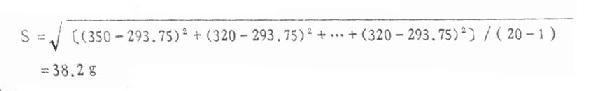
(2)递推法当用电子计算机进行计算,希望每输入一个数据,都能得到X与S,则将式(4.8)与式
(4.5)配合计算。
 (4.15)
(4.15)
这里Sn表示n个数据的标准差,Sn-1表示n-1个数据的标准差。Xn是第n个数据,Xn-1是n-1个数据的均数。
例4.10 仍用例4.3资料,已算得前19例心重的X19=292.37,S19=38.71。X20=320,代入式(4.15)得
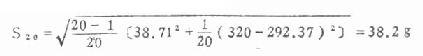
(3)直接法 不需先计算均数,直接用变量值代入式(4.16)或式(1.17)计算。
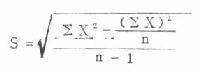 (4.16)
(4.16)
或 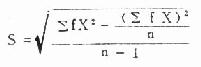 (4.17)
(4.17)
式(4.16)的分子是由式(4.14)的分子简化而得来的,证明如下。
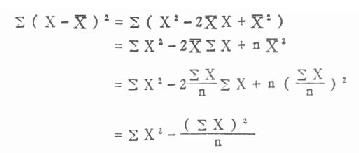
例4.11用ELISA(酶联免疫吸附测定)法检测vero-E6,细胞培养上清正常标本10份的结果(100XOD490值)为2,3,3,4,4,5,5,5,6,8,求标准差。
若用式(4.16)则先计算
∑X=2+3+3+…+6+8=45
∑X2=22+32+32+…62+82=229
若用式(4.17)则先计算
∑fX=1×2+2×3+…+1×6+1×8=45
∑fX2=1×22+2×32+…1×62+1×82=229
然后代入式(4.16)或式(1.17)结果相同。
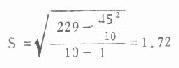
三、变异系数
上述各种变异指标可用来比较同类事物变量值间的变异情况。各变异指标的共同点是:值小表示变量值密集,值大表示变量值分散。但在有些情况下用标准差等变异指标来比较就不适宜了。如某地7岁男童身高均数为123.10cm ,标准差为4.71cm;体重的均数为22.29kg,标准差为2.26kg。由于单位不同,我们不能因为4.71>2.26而说身高的变异大于体重,需要有另一个指标,它不受单位的限制,那就是变异系数,其公式为:
CV=S/X×100%,X>0 (4.18)
也就是将标准差化为各自均数的百分数,然后比较。这样不但可以比较单位不同的变量值间的变异,而且可以比较均数相差悬殊的变量值间的变异。
上述7岁男童身高、体重的变异系数分别为
身高CV=4.17/123.10×100%=3.83%
体重CV=2.26/22.29×100%=10.14%
可见同一批儿童的体重变异比身高的大。
例4.12被试者9人,试验时坐在舒适的牙科椅上测口腔压力波幅PcmAq(厘米水柱)。然后外加呼吸阻力20cmAq(1/sec),5分钟时再测口腔压力波幅结果如下。试比较外加呼吸阻力前后,口腔压力波幅的变异。
表4.9 外加呼吸阻力前后的口腔压力波幅
口腔压力波幅,cmAg
| 口腔压力波幅,cmAg | |||
| X | S | CV(%) | |
| 加阻力前 | 1.218 | 0.256 | 21.019 |
| 加阻力后 | 7.240 | 0.633 | 8.741 |
外阻力前口腔压力波幅的变异较大。
外加呼吸阻力前后的口腔压力波幅的单位都是cmAq,如直接比较两个标准差,可能会得出加阻力后数值变异较大的结论。但由于两均数相差悬殊,加阻力后的均数几乎是加阻力前的6倍,因此就不宜直接比较标准差而应比较它们的变异系数。
变异系数还常用于比较多个样品重复测定的误差等。
运用变异系数时应注意(1)有关的事物间才能作比较,不要将风马牛不相及的东西硬拉在一起作比较;(2)均数小于标准差时应考虑其实际运用价值。因为在这种情况下,可能誇大变异,故不宜使用;(3)比较两变异系数间是否真有差别,亦应作假设检验,不能只看表面值就下结论。
[附]比较两变异系数可用u检验,其公式为
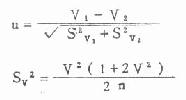
式中V为以小数表示的变异系数,SV2是变异系数的标准误的平方,n是样本含量。u是正态离差系数。
例4.13比较例4.12中两总体变异系数间有无差别。
H0:两总体变异系数相等
H1:两总体变异系数不等
α=0.05

u>u0.05,0.05>P>0.01,在α=0.05的水准处拒绝H0,接受H1,两总体变异系数不等。外加呼吸阻力前的口腔压力波幅的变异较大。
四、运用变异指标的注意事项
1.变异指标表示变量值的变异情况或离中趋势,常与位置指标平均数结合运用,说明变量值集中的位置与离散程度。
2.变异指标种类虽多,但任一变异指标,其值大表示变异大,数值参差甚;值小表示变异小,数值较集中。比较两个或几个同类事物的变异,要用同一变异指标。
3.正态分布资料宜用均数与标准差(有时用方差)描述集中与离散情况,记为X±S。有了均数与标准差就可根据正态分布理论将频数分布描绘出来,进一步可作正常值范围估计与假设检验等(详见第五至第七章),应用较广。为便于计算,正态分布资料亦可用中位数、百分位数和四分位数间距等描述,其结果与用均数、标准差相近。
偏态分布资料宜用中位数及四分位数间距、均差等描述。尤其在资料分布呈明显偏态时,随着例数的增多,中位数、四分位数间距及均差的代表性和稳定性明显优于均数、标准差及方差。
众数和极差只用来对单峰资料作概括的描述。
4. 比较几组资料的变异程度,若各组资料的单位不全相同,或均数相差悬殊时,用变异系数。
5.判断几个方差或变异系数间有无显著差别,需作假设检验,不能只看表面值。详见第七、第八章有关内容。
(胡琳 编)